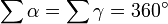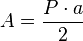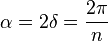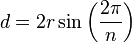Matematicas
viernes, 14 de octubre de 2011
jueves, 18 de agosto de 2011
La circunferencia
Una circunferencia es el conjunto de todos los puntos de un plano que equidistan de otro punto fijo y coplanar llamado centro.
Elementos de la circunferencia
 Secantes, cuerdas y tangentes.
Secantes, cuerdas y tangentes. La mediatriz de una cuerda pasa por el centro de la circunferencia.
La mediatriz de una cuerda pasa por el centro de la circunferencia.- Centro, el punto interior equidistante de todos los puntos de la circunferencia;
- Radio, el segmento que une el centro con un punto cualquiera de la circunferencia;
- Diámetro, el mayor segmento que une dos puntos de la circunferencia (necesariamente pasa por el centro);
- Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros)
- Recta secante, la que corta a la circunferencia en dos puntos;
- Recta tangente, la que toca a la circunferencia en un sólo punto;
- Punto de tangencia, el de contacto de la recta tangente con la circunferencia;
- Arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia;
- Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.
[editar]
Posiciones relativas[editar]
La circunferencia y un puntoUn punto en el plano puede ser:
- Exterior a la circunferencia, si la distancia del centro al punto es mayor que la longitud del radio.
- Perteneciente a la circunferencia, si la distancia del centro al punto es igual a la longitud del radio.
- Interior a la circunferencia, si la distancia del centro al punto es menor a la longitud del radio.
[editar]
La circunferencia y la rectaUna recta, respecto de una circunferencia, puede ser:
- Exterior, si no tienen ningún punto en común con ella y la distancia del centro a la recta es mayor que la longitud del radio.
- Tangente, si la toca en un punto (el punto de tangencia) y la distancia del centro a la recta es igual a la longitud del radio. Una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro.
- Secante, si tiene dos puntos comunes, es decir, si la corta en dos puntos distintos y la distancia del centro a la recta es menor a la longitud del radio.Cuerda que pasa por el centro de la circunferencia
- Segmento circular, es el conjunto de puntos de la regiòn circular comprendida entre una cuerda y el arco correspondiente.
[editar]
Dos circunferenciasDos circunferencias, en función de sus posiciones relativas, se denominan:
- Exteriores, si no tienen puntos comunes y la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 1)
- Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. La distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 2)
- Secantes, si se cortan en dos puntos distintos y la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos. Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto. (Figura 3)
- Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. La distancia que hay entre sus centros es igual al valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra. (Figura 4)
- Interiores excéntricas, si no tienen ningún punto común y la distancia entre sus centros es mayor que 0 y menor que el valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.
- Interiores concéntricas, si tienen el mismo centro (la distancia entre sus centros es 0) y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. (Figura 5)
- Coincidentes, si tienen el mismo centro y el mismo radio. Si dos circunferencias tienen más de dos puntos comunes, necesariamente son circunferencias coincidentes.
[editar]
Ángulos en una circunferencia Ángulos en la circunferencia.
Ángulos en la circunferencia.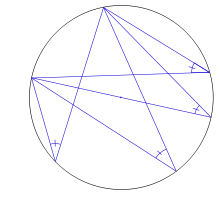 Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.
Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.Un ángulo, respecto de una circunferencia, pueden ser:
Ángulo central, si tiene su vértice en el centro de ésta. Sus lados contienen a dos radios.
- La amplitud de un ángulo central es igual a la del arco que abarca.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.
- La amplitud de un ángulo inscrito en una semi circunferencia equivale a la mayor parte del angúlo exterior que limita dicha base. (Véase: arco capaz.)
Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.
- La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
Ángulo interior, si su vértice está en el interior de la circunferencia.
- La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.
Ángulo exterior, si tiene su vértice en el exterior de la circunferencia
[editar]
Longitud de la circunferenciaLa longitud  de una circunferencia es:
de una circunferencia es:
 de una circunferencia es:
de una circunferencia es:donde  es la longitud del radio.
es la longitud del radio.
 es la longitud del radio.
es la longitud del radio.Pues  (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
(número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
 (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
(número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:[editar]
Ecuaciones de la circunferencia[editar]
Ecuación en coordenadas cartesianasEn un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación
 .
.
Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al
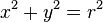 .
.
La circunferencia con centro en el origen y de radio la unidad, es llamadacircunferencia goniométrica, circunferencia unidad o circunferencia unitaria.
De la ecuación general de una circunferencia,
se deduce:
resultando:
Si conocemos los puntos extremos de un diámetro:  ,
,
 ,
,la ecuación de la circunferencia es:
[editar]
Ecuación vectorial de la circunferenciaLa circunferencia con centro en el origen y radio R, tiene por ecuación vectorial:  . Donde
. Donde  es el parámetro de la curva, además cabe destacar que
es el parámetro de la curva, además cabe destacar que  . Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
 . Donde
. Donde  es el parámetro de la curva, además cabe destacar que
es el parámetro de la curva, además cabe destacar que  . Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.[editar]
Ecuación en coordenadas polaresCuando la circunferencia tiene centro en el origen y el radio es c, se describe encoordenadas polares como 

Cuando el centro no está en el origen, sino en el punto 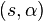 y el radio es
y el radio es  , la ecuación se transforma en:
, la ecuación se transforma en:
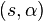 y el radio es
y el radio es  , la ecuación se transforma en:
, la ecuación se transforma en:[editar]
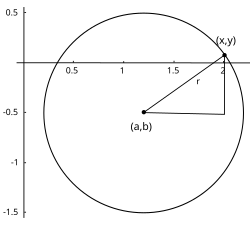
Ecuación en coordenadas paramétricasLa circunferencia con centro en (a, b) y radio c se parametriza con funciones trigonométricas como:
y con funciones racionales como
Poligono Regular
Un polígono regular es un polígono en el que todos los lados tienen la misma longitud y todos los ángulos interiores son de lamisma medida.
- En un polígono regular podemos distinguir:En un polígono regular podemos distinguir:
- Lado, L: es cada uno de los segmentos que forman el polígono.
- Vértice, V: el punto de unión de dos lados consecutivos.
- Centro, C: el punto central equidistante de todos los vértices.
- Radio, r: el segmento que une el centro del polígono con uno de sus vértices.
- Apotema, a: segmento perpendicular a un lado, hasta el centro del polígono.
- Diagonal, d: segmento que une dos vértices no contiguos.
- Perímetro, P: es la suma de la medida de su contorno.
- Semiperímetro, SP: es la mitad de la suma de la suma de la medida de su contorno (mitad del perímetro).
- Lado, L: es cada uno de los segmentos que forman el polígono.
- Vértice, V: el punto de unión de dos lados consecutivos.
- Centro, C: el punto central equidistante de todos los vértices.
- Radio, r: el segmento que une el centro del polígono con uno de sus vértices.
- Apotema, a: segmento perpendicular a un lado, hasta el centro del polígono.
- Diagonal, d: segmento que une dos vértices no contiguos.
- Perímetro, P: es la suma de la medida de su contorno.
- Semiperímetro, SP: es la mitad de la suma de la suma de la medida de su contorno (mitad del perímetro).
las características de los polígonos regularesson de gran utilidad para determinar sus propiedades, y dimensiones geométricas. - Los polígonos regulares son equiláteros; todos sus lados tienen la misma longitud
- Todos los ángulos interiores de un polígono regular tienen la misma medida, es decir, son congruentes
- El centro de un polígono regular es un punto equidistante de todos los vértices del polígono
- Los polígonos se pueden dividir en triángulos cuyos lados son el lado del polígono y los dos segmentos que unen el centro y los vértices (radios)
- El apotema es el segmento que une el centro y la mitad de cada lado del polígono
- El radio es el segmento que une el centro y cada vértice
Todos los polígonos tienen tres o más lados.
[editar]
Los ángulos de un polígono regularEntre los ángulos existentes en un polígono regular, podemos ver: el ángulo central,ángulo interior y ángulo exterior.
[editar]
Ángulos centrales- Todos los ángulos centrales de un polígono regular son congruentes y su medidaα puede obtenerse a partir del número de lados n del polígono
 en radianes
en radianes
[editar]
Ángulos interiores- El Ángulo interior,
 , de un polígono regular mide:
, de un polígono regular mide:
 en grados sexagesimales
en grados sexagesimales
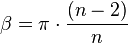 en radianes
en radianes
- La suma de los ángulos interiores,
 , de un polígono regular es de:
, de un polígono regular es de:
 en grados sexagesimales
en grados sexagesimales
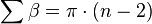 en radianes
en radianes
[editar]
Ángulos exteriores- El Ángulo exterior,
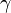 , de un polígono regular es de:
, de un polígono regular es de:
 en grados sexagesimales
en grados sexagesimales
 en radianes
en radianes
- La suma de los ángulos exteriores,
 , de un polígono regular es:
, de un polígono regular es:
 en grados sexagesimales
en grados sexagesimales
 en radianes
en radianes
Como puede verse la suma de los ángulos exteriores de un polígono, y de un polígono regular en particular, mide una circunferencia completa, independientemente del número de lados.
A esta conclusión se podía llegar percatándose de que:
dado que todos los ángulos interiores de un triángulo suman 180 grados, que resulta:
Por otro lado al ser ángulos suplementarios tenemos:
por tanto, en un polígono regular el ángulo central y el exterior miden lo mismo:
y habiendo el mismo número de ángulos centrales y exteriores en un polígono, su suma también es la misma:
que es una circunferencia completa, independientemente del número de lados, esta conclusión es valida también para los polígonos no regulares.
[editar]
Galería de polígonos regulares- Triángulo equilátero(Triángulo regular).
- Cuadrado (cuadriláteroregular).
- Pentágono regular.
- Hexágono regular.
- Heptágono regular.
- Octágono regular.
- Eneágono regular.
- Decágono regular.
- Endecágono regular.
- Dodecágono regular.
- Tridecágono regular.
- Tetradecágono regular.
[editar]
Área de los polígonos regularesPara calcular el área, A, de un polígono debemos multiplicar el perímetro, P, por el apotema, a, y dividido entre dos. Lo que se resume con la siguiente formula matematica:
Partiendo del triángulo que tiene por base un lado,L, del polígono y altura su apotema,a , el área de este triángulo, es:
Un polígono de n lados, tiene n de estos triángulos, por lo tanto el área del polígono será:
esto es:
Sabiendo que la longitud de un lado,L, por el número,n, de lados es el perímetro,P , tenemos:
[editar]
Área de un polígono regular, conociendo el número de lados y la apotemaSabiendo que:

Además  , ya que es la mitad de un ángulo central (esto en radianes).
, ya que es la mitad de un ángulo central (esto en radianes).
 , ya que es la mitad de un ángulo central (esto en radianes).
, ya que es la mitad de un ángulo central (esto en radianes).Observando la imagen, es posible deducir que 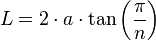
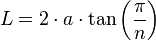
Sustituyendo el lado:

Finalmente:

Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.
[editar]
Área de un polígono, conociendo el número de lados y el radioUn polígono queda perfectamente definido por su número de lados n, y el radio r, por tanto podemos determinar cual es su área, a la vista de la figura, tenemos que:
donde el ángulo central es:
sabiendo que el área de un polígono es:
y sustituyendo el valor del lado y la apotema calculados antes, tenemos:
ordenando tenemos:
sabiendo que:
resulta:
o lo que es lo mismo:
Con esta expresión podemos calcular el área del polígono, conociendo solamente el número de lados y su radio, lo que resulta útil en muchos casos.
[editar]
Área de un polígono en función del ladoY si queremos expresar el área en función del lado, podemos calcularlo de la siguiente manera:
Sea  el ángulo formado por el Lado "L" y el radio "r":
el ángulo formado por el Lado "L" y el radio "r":
 el ángulo formado por el Lado "L" y el radio "r":
el ángulo formado por el Lado "L" y el radio "r":El valor de la apotema en función del lado será, por la definición de la tangente:
Despejando la apotema tenemos:
Sustituimos la apotema por su valor:
Con lo que conociendo el número de lados del polígono regular y la longitud del lado podemos calcular su superficie.
[editar]
Diagonales de un polígono regularComo ya se ha dicho la diagonal de un polígono es el segmento que une dos vértices no contiguos, vamos a ver algunas características de estas diagonales.
[editar]
Número de diagonalesPara determinar el número de diagonales Nd, de un polígono de n vértices realizaremos el siguiente razonamiento:
- De un vértice cualquiera partirán (n – 3) diagonales, donde n es el número de vértices, dado que no hay ningún diagonal que le una consigo mismo ni con ninguno de los dos vértices contiguos.
- Esto es valido para los n vértices del polígono.
- Una diagonal une dos vértices, por lo que aplicando el razonamiento anterior tendríamos el doble de diagonales de las existentes.
Según el razonamiento tendremos que:
[editar]
Longitud de la diagonal más pequeñaLa diagonal más pequeña de un polígono regular es la que une dos vértices alternos, para determinar su longitud, partimos del ángulos central y del radio, el radio que pasa por el vértice intermedio, corta a la diagonal en el punto A, este radio y la diagonal son perpendiculares en A.
Esto es el triángulo VAC es rectángulo en A, por tanto:
que resulta:
de donde deducimos que:
Sabiendo el valor del ángulo central:
La diagonal más pequeña de un polígono regular, solo depende del radio y del número de lados, siendo tanto mayor cuanto mayor sea el radio y disminuyendo de longitud cuando aumenta el número de lados del polígono.
Suscribirse a:
Entradas (Atom)





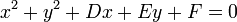







![x=a + c \cos t,\ y=b+c\sin t,\qquad t\in[0,2\pi]](http://upload.wikimedia.org/math/f/d/0/fd08b31a7dac369664c95f143fb10657.png)


 en
en